图的表示
G = (V, E),分为有向图和无向图
有两种表示方法
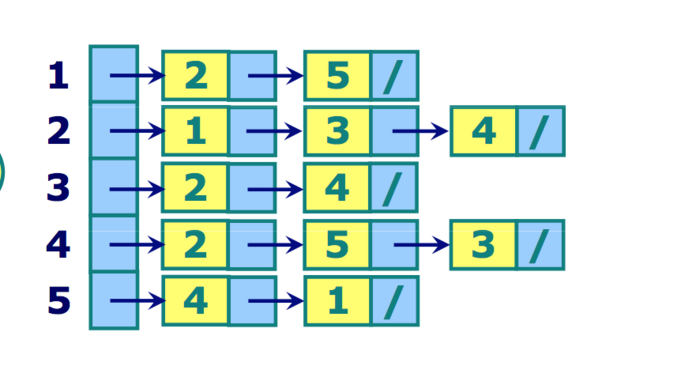
- 邻接链表
- 常用于表示稀疏图(
E远小于V^2) - 空间需求为
O(V+E) - 无法快速判断是否包含一条边
- 常用于表示稀疏图(
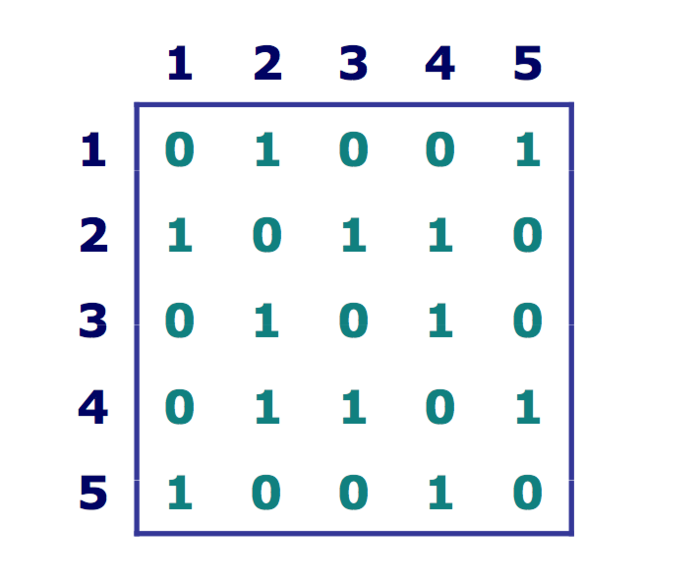
- 邻接矩阵
- 更简单
- 空间需求为
O(V^2) - 可以快速判断任意两个节点间是否有边
- 对无向图而言,只需要一半的存储空间
图的表示(Java)
无权无向图
package graph;
import java.util.ArrayList;
import java.util.LinkedList;
public class Graph {
private int nodeNum;
private LinkedList<Integer>[] adj; // 邻接链表表示边
private ArrayList<Node> nodes; // 所有节点
public Graph(int nodeNum) {
this.nodeNum = nodeNum;
this.adj = new LinkedList[nodeNum];
for (int i = 0; i < nodeNum; i++) {
this.adj[i] = new LinkedList<>();
}
this.nodes = new ArrayList<>();
}
public void addNode(Node a) {
this.nodeNum++;
this.nodes.add(a);
}
public void addEdge(Node a, Node b) {
if (!this.adj[a.getId()-1].contains(b.getId())) {
this.adj[a.getId()-1].add(b.getId());
}
if (!this.adj[b.getId()-1].contains(a.getId())) {
this.adj[b.getId()-1].add(a.getId());
}
}
public Node getNode(int id) {
Node node = null;
for(Node n: this.nodes) {
if (n.getId() == id) {
node = n;
break;
}
}
return node;
}
public static void main(String[] args) {
}
}
class Node {
private int id;
private int data; // 卫星数据
private int key; //
private Node pre;
public Node(int id) {
this.setId(id);
this.setData(id);
this.setKey(Integer.MAX_VALUE);
this.setPre(null);
}
public int getId() {
return id;
}
public void setId(int id) {
this.id = id;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public int getKey() {
return key;
}
public void setKey(int key) {
this.key = key;
}
public Node getPre() {
return pre;
}
public void setPre(Node pre) {
this.pre = pre;
}
}
广度优先遍历(BFS)
- 给定图
G = (V, E)和一个可识别的源节点S,BFS对G中的边进行探索来发现所有可以从S到达的节点,并计算出相应的距离。 - BFS始终在发现所有距离源节点
S为k的所有节点后,再发现距离源节点S为k+1的其他节点 - BFS需要维护一个
visited的布尔数组,用于记录每个节点是否被访问过,每个节点至多被访问一次,至多有一个父节点 - 大致思路
- 初始化
visited布尔数组,开始时对所有节点标记为false - 初始化每个节点的
key为Integer.MAX_VALUE,key表示从源节点到该节点经过的边数。 - 初始化每个节点的
pre为null,标识为每个节点的前驱节点 - 维护一个队列,将源节点加入队列
- 循环将队列头的节点出列,对每个出列的节点,修改
visited为true。若与其相连的节点未被访问过,则加入队列中
- 初始化
- 时间复杂度
O(V + E),初始化操作为O(V),遍历链表O(E) - 可用于找到单源最短路径,但是边的权重为单位权重1
- 队列实现
public void bfs() { LinkedList<Node> go = new LinkedList<>(); boolean[] visited = new boolean[this.nodeNum]; go.add(this.nodes.get(0)); visited[this.nodes.get(0).getId()-1] = true; while(go.size() != 0) { Node cur = go.removeFirst(); System.out.println(cur.getId()); for(int i: this.adj[cur.getId()-1]) { Node next = this.getNode(i); if (!visited[next.getId()-1]) { go.add(next); visited[next.getId()-1] = true; } } } }
深度优先遍历(DFS)
- DFS总是对最近才发现的节点
v的出发边进行探索,直到该节点的所有出发边都被发现为止。一旦当前节点的所有边对应的节点都已被发现,则搜索回溯到当当前节点的前驱节点。直到所有节点都被发现。 - 时间复杂度
O(V + E),初始化操作为O(V),遍历链表O(E) - 可通过递归或栈迭代实现
递归
public void dfs() { boolean[] visited = new boolean[this.nodeNum]; for(Node n: this.nodes) { if(!visited[n.getId()-1]) { this.dfsVisit(n, visited); } } } public void dfsVisit(Node node, boolean[] visited) { visited[node.getId()-1] = true; System.out.println(node.getId()); for(int i: this.adj[node.getId()-1]) { Node next = this.getNode(i); if (!visited[next.getId()-1]) { dfsVisit(next, visited); } } }栈
- 遍历当前节点的所有边,若边对应的节点未被发现,则将对应的节点入栈,并跳出遍历;若当前节点的所有边都已被发现,则将当前节点出栈
public void dfsStack() { Stack<Node> stack = new Stack<>(); boolean[] visited = new boolean[this.nodeNum]; stack.add(this.getNode(1)); visited[0] = true; System.out.println(1); while(!stack.isEmpty()) { Node n = stack.peek(); // NO POP boolean popTop = true; for(int i=0;i<this.adj[n.getId()-1].size();i++) { Node temp = this.getNode(this.adj[n.getId()-1].get(i)); if(!visited[temp.getId()-1]) { stack.push(temp); visited[temp.getId()-1] = true; popTop = false; System.out.println(temp.getId()); break; } } if(popTop) { stack.pop(); } } }
拓扑排序(Topological Sort)
- 针对有向无环图
G(V, E),拓扑排序是G中所有节点的一种线性次序,包含如下条件:如果图G包含边(u, v),则节点u在拓扑排序中处于节点v的前面 - 可通过DFS实现:初始化一个队列,对G中所有节点进行DFS,在每个节点完成所有边的探查后将该节点插入到队列头部
- 对于递归实现的DFS,在
dfsVisit函数结束前执行list.addFirst(node); - 对于栈实现的DFS,在
pop在节点的时候执行list.addFirst(node);
最小生成树
Kruskal算法和Prim算法,时间复杂度都在O(E*lgV)。如果用斐波那契堆,Prim算法的时间复杂度将改善为O(E+V*lgV)。- 两种算法都是贪心算法
Prim算法
- 从任意根节点
r开始,每一次选择r所在的连通集合 与该集合外 相连的所有边中权值最小的,将该条边不在连通集合中的那个点加入到连通集合中。选择的这条边要保证在加入后不会形成环路 - 实际算法执行的大致思路
- 为每一个节点设置一个
key值,该值表示该点到连通集合的最短边的权重,初始设置为∞。为每一个节点设置一个π值,表示该点的被添加进连通集合时的前驱节点。设置根节点的key值为0 - 将树种所有节点加入到一个集合
Q中,每一次在Q中选出一个key值最小的节点,并将该节点加入到连通集合中。对该节点所有的边进行遍历,若对应的节点在Q中并且其key值大于了该条边的权重,则更新对应节点的key值为该条边的权重。 - 重复选取
key值最下的节点直到Q为空
- 为每一个节点设置一个
- 时间复杂度分析
Time(Total) = O(V) * Time(Extract-min) + O(E) * Time(Decrease-key)
| Q | Time(Extract-min) | Time(Decrease-key) | Total |
|---|---|---|---|
| Array | O(V) | O(1) | O(V^2) |
| Binary Heap | O(lgV) | O(lgV) | O(ElgV) |
Kruskal算法
- 该算法是从边入手的。首先将所有的边按照权重从小到大排序。
O(E * lg E) - 初始创建
|V|棵树,每棵树都只包含一个节点。树可以用set表示。O(1) - 每一个从边的集合中选取一个权值最小的边,判断边的两个顶点是否在一个
set中,若在则放弃该边继续找下一个。若不在,则将两个顶点所在的set合并在一起。重复处理完所有的边O(E * lgV) - 时间复杂度为
O(E * lgV)。具体在算法导论原书P631 - 下面代码实现中没有实现边的最小堆
package graph;
import java.util.ArrayList;
import java.util.Collection;
import java.util.Collections;
import java.util.HashMap;
import java.util.HashSet;
import java.util.LinkedList;
import java.util.Map;
public class WeightedGraph {
private int nodeNum;
private int[][] adj;
private ArrayList<Node> nodes;
public WeightedGraph(int nodeNum) {
this.nodeNum = nodeNum;
this.adj = new int[nodeNum][nodeNum];
for (int i = 0; i < nodeNum; i++) {
for (int j = 0; j < nodeNum; j++) {
this.adj[i][j] = Integer.MAX_VALUE;
}
}
this.nodes = new ArrayList<>();
}
public void addNode(Node a) {
this.nodes.add(a);
}
public void addEdge(Node a, Node b, int len) {
this.adj[a.getId() - 1][b.getId() - 1] = len;
this.adj[b.getId() - 1][a.getId() - 1] = len;
}
public Node getNode(int id) {
Node node = null;
for (Node n : this.nodes) {
if (n.getId() == id) {
node = n;
break;
}
}
return node;
}
public int naivePrim(int startId) {
LinkedList<Node> go = new LinkedList<>();
go.add(this.getNode(startId));
int sum = 0;
while (go.size() != this.nodeNum) {
int minEdge = Integer.MAX_VALUE;
int nextNodeId = -1;
for (Node node : go) {
for (int i=0;i<this.nodeNum;i++) {
if (!go.contains(this.getNode(i+1)) && this.adj[node.getId()-1][i] <= minEdge) {
nextNodeId = i+1;
minEdge = this.adj[node.getId()-1][i];
}
}
}
if (nextNodeId != -1) {
go.add(this.getNode(nextNodeId));
sum += minEdge;
System.out.println(nextNodeId + " "+ minEdge);
minEdge = Integer.MAX_VALUE;
}
}
return sum;
}
public void prim(int startId) {
// key值是连接该节点与树的最小的边的权重
for(Node n: this.nodes) {
n.setKey(Integer.MAX_VALUE);
}
// go为所有未加入树的节点
LinkedList<Node> go = new LinkedList<>();
go.addAll(this.nodes);
go.get(0).setKey(0);
while(go.size() != 0) {
// 选择key值最小的
Node next = null;
int minKey = Integer.MAX_VALUE;
for (Node node : go) {
if(node.getKey() <= minKey) {
minKey = node.getKey();
next = node;
}
}
go.remove(next);
System.out.println(next.getId() + " " + next.getKey());
// 更新与next节点相连节点的key值
for(int i=0;i<this.nodeNum;i++) {
Node find = this.getNode(i+1);
if(go.contains(find) && this.adj[next.getId()-1][i] < find.getKey()) {
find.setKey(this.adj[next.getId()-1][i]);
find.setPre(next);
}
}
}
}
public void kruskal(int startId) {
LinkedList<Node> go = new LinkedList<>();
ArrayList<HashSet<Node>> allSet = new ArrayList<>();
for(Node node: this.nodes) {
HashSet<Node> temp = new HashSet<>();
temp.add(node);
allSet.add(temp);
}
// TODO:按照边的权重从小到大排序
HashMap<Node[], Integer> edges = new HashMap<>();
for(int i=0; i<this.nodeNum; i++) {
for(int j=i+1; j<this.nodeNum; j++) {
Node[] tem = {getNode(i+1), getNode(j+1)};
edges.put(tem, this.adj[i][j]);
}
}
while(edges.size() != 0) {
Node[] n = null;
int weight = Integer.MAX_VALUE;
// 选权重最小的边
for(Node[] ns: edges.keySet()) {
if (edges.get(ns) <= weight) {
weight = edges.get(ns);
n = ns;
}
}
edges.remove(n);
HashSet<Node> aSet = null;
HashSet<Node> bSet = null;
for(HashSet<Node> tempSet: allSet) {
if(tempSet.contains(n[0])) {
aSet = tempSet;
}
if(tempSet.contains(n[1])) {
bSet = tempSet;
}
}
if(aSet == bSet) {
continue;
}
go.add(n[0]);
go.add(n[1]);
aSet.addAll(bSet);
allSet.remove(bSet);
System.out.println(weight);
}
// for(Node n : go) {
// System.out.println(n.getId());
// }
}
public static void main(String[] args) {
WeightedGraph graph = new WeightedGraph(9);
Node node1 = new Node(1);graph.addNode(node1);
Node node2 = new Node(2);graph.addNode(node2);
Node node3 = new Node(3);graph.addNode(node3);
Node node4 = new Node(4);graph.addNode(node4);
Node node5 = new Node(5);graph.addNode(node5);
Node node6 = new Node(6);graph.addNode(node6);
Node node7 = new Node(7);graph.addNode(node7);
Node node8 = new Node(8);graph.addNode(node8);
Node node9 = new Node(9);graph.addNode(node9);
graph.addEdge(node1, node2, 4);
graph.addEdge(node2, node3, 8);
graph.addEdge(node3, node4, 7);
graph.addEdge(node4, node5, 9);
graph.addEdge(node5, node6, 10);
graph.addEdge(node6, node7, 2);
graph.addEdge(node7, node8, 1);
graph.addEdge(node8, node9, 7);
graph.addEdge(node1, node8, 8);
graph.addEdge(node2, node8, 11);
graph.addEdge(node3, node9, 2);
graph.addEdge(node3, node6, 4);
graph.addEdge(node4, node6, 14);
graph.addEdge(node7, node9, 6);
// graph.prim(1);
graph.kruskal(1);
}
}
单源最短路径
| Algorithms| Unweighted | Positive | Negative | Cycle | Time | |:–:|:–:|:–:|:–:|:–:|:–:| | Breath-First Search| √ | × | × | √ | O(V + E) | | Dag Shortest Paths | √ | √ | √ | × | O(V + E) | | Dijkstra | √ | √ | × | √ | O(ElgV) | | Bellman-Ford | √ | √ |√ | √ | O(VE) |
Bellman-Ford
- Bellman-Ford返回一个布尔值,以表明是否存在一个从源节点可以到达的权重为负值的环路。如果存在这样一个环路,返回false,否则算法将给出最短路径及其权重
- Bellman-Ford通过对边的松弛操作来逐渐降低从源节点到每个节点的最短路径。
- 大致思路
- 算法首先将每个顶点的
d和π分别初始为∞和null,分别代表源点到该顶点的最短路径和该顶点的前驱节点 - 对每条边进行
|V| -1次松弛操作(一次松弛最多进过0个点的最短路径,两次松弛最多经过1个点的最短路径。路径长度最长为V,最多经过V-2,最多松弛V-1) - 对每条边
(u, v)检查v.d > u.d + w(u, v),若有一条边上式成立则表示存在负权环路,返回false
- 算法首先将每个顶点的
- 时间复杂度为
O(V*E)
Dag Shortest Paths
- 该算法利用到了拓扑排序,减少对边松弛的总次数
- 拓扑排序后,对序列中的节点从头到尾进行遍历,对每一个节点的边进行一次松弛操作
- 时间复杂度为
O(V + E),拓扑排序为O(V + E),初始化为O(V),松弛为O(E)
Dijkstra
- 思路类似于Prim算法
- 维系一个集合S,从原节点s到S所有节点间的最短路径已经找到
- 将所有节点加入Q,每一次从Q中选择一个d值最小的节点,将该节点加入到S中,并对该节点的所有边进行松弛操作
- 时间复杂度为
O(E*lgV),与Prim算法类似
package graph;
import java.util.ArrayList;
import java.util.LinkedList;
public class DirectedGraph {
private int nodeNum;
private int[][] adj;
private ArrayList<Node> nodes;
private int[][] minPath;
private int[][] preMatrix;
public DirectedGraph(int nodeNum) {
this.nodeNum = nodeNum;
this.adj = new int[nodeNum][nodeNum];
this.minPath = new int[nodeNum][nodeNum];
this.preMatrix = new int[nodeNum][nodeNum];
for (int i = 0; i < nodeNum; i++) {
for (int j = 0; j < nodeNum; j++) {
this.adj[i][j] = i==j?0:Integer.MAX_VALUE;
this.minPath[i][j] = this.adj[i][j];
this.preMatrix[i][j] = -1;
}
}
this.nodes = new ArrayList<>();
}
public void addNode(Node a) {
this.nodes.add(a);
}
public void addEdge(Node a, Node b, int len) {
this.adj[a.getId() - 1][b.getId() - 1] = len;
this.minPath[a.getId() - 1][b.getId() - 1] = len;
this.preMatrix[a.getId() - 1][b.getId() - 1] = a.getId();
}
public Node getNode(int id) {
Node node = null;
for (Node n : this.nodes) {
if (n.getId() == id) {
node = n;
break;
}
}
return node;
}
public boolean bellmanford(Node startNode) {
startNode.setKey(0);
// 对所有的边进行V-1次松弛
// 一次松弛最多进过0个点的最短路径,两次松弛最多经过1个点的最短路径
// 路径长度最长为V,最多经过V-2,最多松弛V-1
for(int relaxNum=0; relaxNum<this.nodeNum-1; relaxNum++) {
boolean relax = false; // 优化
// each edge
for(int i=0;i<this.nodeNum;i++) {
for(int j=0;j<this.nodeNum;j++) {
// relax
int weight = this.adj[i][j];
Node n1 = this.getNode(i+1);
Node n2 = this.getNode(j+1);
if (weight == Integer.MAX_VALUE || n1.getKey() == Integer.MAX_VALUE) {
continue;
}
if(n1.getKey() + weight < n2.getKey()) {
n2.setKey(n1.getKey()+weight);
n2.setPre(n1);
}
relax = true;
}
}
if(!relax) {
break;
}
}
// 检测负权回路
for(int i=0;i<this.nodeNum;i++) {
for(int j=0;j<this.nodeNum;j++) {
int weight = this.adj[i][j];
Node n1 = this.getNode(i+1);
Node n2 = this.getNode(j+1);
if(weight!=Integer.MAX_VALUE && n1.getKey() + weight < n2.getKey()) {
return false;
}
}
}
return true;
}
public void dagShortestPath(Node startNode) {
startNode.setKey(0);
LinkedList<Node> topologicallySort = this.topologicallySort();
for(Node n: topologicallySort) {
for(int i=0;i<this.nodeNum;i++) {
int weight = this.adj[n.getId()-1][i];
if(weight == Integer.MAX_VALUE) {
continue;
}
Node next = this.getNode(i+1);
if(n.getKey() != Integer.MAX_VALUE && next.getKey() > n.getKey() + weight) {
next.setKey(n.getKey() + weight);
next.setPre(n);
}
}
}
}
public LinkedList<Node> topologicallySort(){
LinkedList<Node> go = new LinkedList<>();
boolean[] visited = new boolean[this.nodeNum];
for(int i=0;i<this.nodeNum;i++) {
if(!visited[i]) {
dfsVisit(this.getNode(i+1), visited, go);
}
}
return go;
}
public void dfsVisit(Node node, boolean[] visited, LinkedList<Node> go) {
visited[node.getId()-1] = true;
for(int j=0; j<this.nodeNum; j++) {
if(this.adj[node.getId()-1][j] != Integer.MAX_VALUE && !visited[j]) {
dfsVisit(this.getNode(j+1), visited, go);
}
}
go.addFirst(node);
}
public void dijkstra(Node startNode) {
LinkedList<Node> go = new LinkedList<>();
go.addAll(this.nodes);
startNode.setKey(0);
while(go.size() != 0) {
// find最小key节点
Node next = null;
int minKey = Integer.MAX_VALUE;
for (Node node : go) {
if(node.getKey() <= minKey) {
minKey = node.getKey();
next = node;
}
}
go.remove(next);
// relax相邻节点
for(int i=0;i<this.nodeNum;i++) {
int weight = this.adj[next.getId()-1][i];
if(weight != Integer.MAX_VALUE && this.getNode(i+1).getKey() > weight+next.getKey()) {
this.getNode(i+1).setKey(weight+next.getKey());
this.getNode(i+1).setPre(next);
}
}
}
}
public static void main(String[] args) {
// 这里mock的数据是用于 所有节点对的最短路径问题
DirectedGraph graph = new DirectedGraph(5);
Node node1 = new Node(1);graph.addNode(node1);
Node node2 = new Node(2);graph.addNode(node2);
Node node3 = new Node(3);graph.addNode(node3);
Node node4 = new Node(4);graph.addNode(node4);
Node node5 = new Node(5);graph.addNode(node5);
graph.addEdge(node1, node2, 3);
graph.addEdge(node1, node3, 8);
graph.addEdge(node1, node5, -4);
graph.addEdge(node2, node4, 1);
graph.addEdge(node2, node5, 7);
graph.addEdge(node3, node2, 4);
graph.addEdge(node4, node1, 2);
graph.addEdge(node4, node3, -5);
graph.addEdge(node5, node4, 6);
// for bellmanford
// boolean re = graph.bellmanford(node1);
// System.out.println(re);
// for(Node n: graph.nodes) {
// if (n.getPre() == null) {
// System.out.println(n.getId() + " " + n.getKey() + " null");
// } else {
// System.out.println(n.getId() + " " + n.getKey() + " " + n.getPre().getId());
// }
//
// }
// for dagShortestPath
// graph.dagShortestPath(node5);
// for(Node n: graph.nodes) {
// if (n.getPre() == null) {
// System.out.println(n.getId() + " " + n.getKey() + " null");
// } else {
// System.out.println(n.getId() + " " + n.getKey() + " " + n.getPre().getId());
// }
//
// }
// for dijkstra
// graph.dijkstra(node1);
// for(Node n: graph.nodes) {
// if (n.getPre() == null) {
// System.out.println(n.getId() + " " + n.getKey() + " null");
// } else {
// System.out.println(n.getId() + " " + n.getKey() + " " + n.getPre().getId());
// }
//
// }
}
}
# 所有节点对的最短路径
| Algorithms| Time | Data Structure |
|:–:|:–:|:–:|
| Brute-Force
(Run Bellman-Ford once from each vertex) | O(V^2 * E) |Adjacency list / array |
| Dynamic programming |O(V^4) |Adjacency array |
| Improved dynamic programming | O(V^3 * lgV)|Adjacency array |
| Floyed-Warshell algorithm |O(V^3) |Adjacency array |
| Johnson algorithm | O(VElgV)|Adjacency list / array |
Floyed-Warshell algorithm
- 可以存在负权重的边,但不能有权重为负数的环路
- 算法思路大概是从
i到j有一条路,假设节点k是该路上的一点,那么d(i, j) = Min(d(i, k)+d(k, j), d(i, j) )。所以使得k = 1 to n,三层循环自底向上完成所有的解
算法
public void floyedWarshall() {
int num = this.nodeNum;
for(int k=0; k<num; k++) {
for(int i=0; i<num; i++) {
for(int j=0; j<num; j++) {
if (this.minPath[i][k] != Integer.MAX_VALUE && this.minPath[k][j] != Integer.MAX_VALUE) {
if (this.minPath[i][j] > this.minPath[i][k] + this.minPath[k][j]) {
this.minPath[i][j] = this.minPath[i][k] + this.minPath[k][j];
this.preMatrix[i][j] = k+1;
}
}
}
}
}
}
测试
// for floyedWarshall
graph.floyedWarshall();
for(int i=0; i<graph.nodeNum; i++) {
for(int j=0; j<graph.nodeNum; j++) {
System.out.print(graph.minPath[i][j] + " ");
}
System.out.println();
}
System.out.println();
for(int i=0; i<graph.nodeNum; i++) {
for(int j=0; j<graph.nodeNum; j++) {
System.out.print(graph.preMatrix[i][j] + " ");
}
System.out.println();
}
用于稀疏图的Johnson algorithm
- 重新赋予权重
- 如果G中所有边的权重均为非负数,那么可对所有节点运行一次Dijkstra算法
- 如果有权重为负的边,那么需要首先添加一个额外的节点,该节点到图中所有其他节点的距离均为0,然后以该节点为源节点,用Bellman-Ford算法运行一次,得到该额外节点到其他所有节点的最短路径,每一个值即为h。
- 则新的权重为
w'(u, v) = w(u, v) + h(u) - h(v) - 新的图中所有原来的边都为非负值,对所有节点运行Dijkstra算法,得到最短路径
δ'(u, v),则原来的最短路径d(u ,v) = δ'(u, v) + h(v) - h(u)
算法
DirectedGraph plusGraph = new DirectedGraph(graph.nodeNum+1);
for(Node n: graph.nodes) {
plusGraph.addNode(n);
}
// 添加额外节点
Node nodeP = new Node(6);plusGraph.addNode(nodeP);
for(int i=0;i<graph.nodeNum;i++) {
for(int j=0;j<graph.nodeNum;j++) {
plusGraph.adj[i][j] = graph.adj[i][j];
}
}
for(int i=0;i<graph.nodeNum+1;i++) {
plusGraph.adj[graph.nodeNum][i] = 0;
plusGraph.adj[i][graph.nodeNum] = Integer.MAX_VALUE;
}
// run bellmanford
boolean runRet = plusGraph.bellmanford(nodeP);
if(!runRet) {
System.out.println("The input graph contaions a negative-weight cycle");
}
// key part
for(int i=0;i<graph.nodeNum;i++) {
for(int j=0;j<graph.nodeNum;j++) {
if (graph.adj[i][j] != Integer.MAX_VALUE) {
graph.adj[i][j] += plusGraph.getNode(i+1).getKey() - plusGraph.getNode(j+1).getKey();
}
}
}
ArrayList<Integer> h = new ArrayList<>();
for(Node node: graph.nodes) {
h.add(node.getKey());
node.setKey(Integer.MAX_VALUE);
}
// key part
for(Node node: graph.nodes) {
graph.dijkstra(node);
for(int i=0;i<graph.nodeNum;i++) {
graph.minPath[node.getId()-1][i] = graph.getNode(i+1).getKey() + h.get(i) - h.get(node.getId()-1);
graph.getNode(i+1).setKey(Integer.MAX_VALUE);
}
}
// print result
for(int i=0; i<graph.nodeNum; i++) {
for(int j=0; j<graph.nodeNum; j++) {
System.out.print(graph.minPath[i][j] + " ");
}
System.out.println("__" + graph.getNode(i+1).getKey());
}